Интересные задания с физических олимпиад с ответами

1.     Однородный стержень массой 6 кг и длиной 80 см подвешен на двух нитях длиной 50 см каждая.
Нити привязаны к концам стержня и закреплены в одной точке на потолке.
Каково при этом натяжение каждой из нитей? g = 10 м/с2.

2.
     На парашютиста массой 80 кг в начале прыжка действует сила сопротивления воздуха, вертикальная составляющая которой 400 Н, а горизонтальная 300 Н.
Найдите равнодействующую всех сил. g = 10 м/с2.

3.
     На концах стержня массой 3 кг и длиной 0,9 м закреплены грузы массами 1 кг и 5 кг.
Стержень подвешен на нити и расположен горизонтально.
Найти расстояние от более легкого груза до точки подвеса.
     Ответ:      0,65 м.

4.
     К телу, имеющему ось вращения, приложен момент сил 25 Нм.
Какое плечо должна иметь тормозящая сила 50 Н, чтобы тело не вращалось?
     Ответ:      50 см.

5.
     Доска, массой 8,5 кг, приставлена к стене так, что образует с полом угол 60°.
Какую минимальную горизонтальную силу нужно приложить к верхнему краю доски, чтобы она не давила на стену?
     Ответ:      25 Н.

6.
     К концам однородного стержня массой 2 кг и длиной 0,6 м подвешены грузы массами 4 кг и 2 кг.
На каком расстоянии от груза большей массы нужно шарнирно закрепить горизонтальный стержень, чтобы он находился в равновесии?
     Ответ:     0,225 м.

7.
     Однородный брус массой 60 кг и длиной 20 м лежит горизонтально на двух опорах, расположенных на расстоянии 3 м от левого и правого краев бруса.
Определить максимальную массу человека, который может дойти до края бруса, не нарушив равновесия.
     Ответ:      140 кг.

8.
     Однородная балка лежит на столе так, что ¾ ее длины находится на столе.
К свешивающемуся концу прикладывают силу, направленную вертикально вниз.
Когда значение силы стало равно 160 Н, противоположный конец балки приподнялся.
Найдите массу балки.
     Ответ:      16 кг.

9.
     Под каким наибольшим углом к вертикали может стоять лестница, прислоненная к гладкой вертикальной стене, если коэффициент трения лестницы о пол 0,5?
Центр тяжести лестницы находится в ее середине.
     Ответ:      45˚.

10.
     Однородная балка массой 60 кг упирается в угол между стенкой и полом.
Угол наклона балки к горизонту равен 30˚.
Верхний конец балки соединен канатом со стенкой. Найдите силу натяжения каната, если угол между балкой и канатом 60˚.
Массой каната пренебречь.
     Ответ:     300 Н.

11.
     Два мальчика массами 50 кг и 35 кг сидят на концах легкой доски длиной 3,6 м, перекинутой через опору, расположенную посередине доски.
На каком расстоянии от опоры должен сесть третий мальчик массой 25 кг, чтобы доска находилась в равновесии?
     Ответ:      1,08 м.

12.
     Под действием силы тяжести груза и силы F = 120 Н рычаг, представленный на рисунке, находится в равновесии.
Вектор силы перпендикулярен рычагу.
Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на горизонтальную и вертикальную оси, представлены на рисунке.
Найти массу груза?

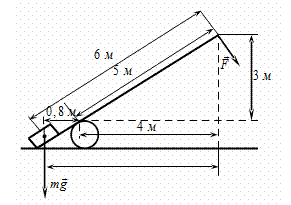
     Ответ:      75 кг.

13.
     Два однородных шара диаметром 0,6 м каждый скреплены в точке касания их поверхностей.
На каком расстоянии от точки касания находится центр масс системы, если масса одного шара в 3 раза больше массы другого?
     Ответ:     0,15 м.

14.
     К легкому рычагу сложной формы имеющему равновеликие стороны, с осью вращения в точке О (см. рис.) подвешен груз массой 1 кг и прикреплена пружина, второй конец которой прикреплен к неподвижной стене.
Рычаг находится в равновесии, чему равна сила упругости пружины?

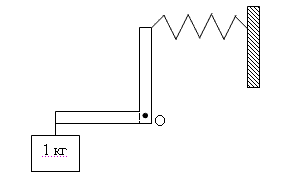
     Ответ:     10 Н.

15.
     Что труднее удержать в воде: кирпич или кусок железа, если они имеют одинаковые массы?
     Ответ:      Кусок железа удержать труднее.

16.
     В баке высотой 1 м находится керосин.
Найти давление керосина на дно бака. Плотность керосина 800 кг/м³.
     Ответ:     8 кПа.

17.
     Стеклянная трубка с одним запаянным концом длиной 1 м, расположена под углом к горизонту так, что длина столбика воды в трубке составляет 90 см, а поверхность воды в трубке расположена на высоте 80 см от пола.
Чему равно давление воды на дно трубки?
     Ответ:     8 кПа.

18.
     В подводной части судна на глубине 6 м образовалось отверстие площадью 20 см².
Какую минимальную силу нужно приложить, чтобы удержать заплату, закрывающую отверстие изнутри?
     Ответ:      120 Н.

19.
     Определить давление, оказываемое средой на батискаф, находящийся в океане на глубине 70 метров.
Плотность морской воды 1030 кг/м³, атмосферное давление нормальное.
     Ответ:      821 кПа.

20.
     Плотность некоторого однородного тела в 1,25 раза больше плотности воды. Во сколько раз вес этого тела в воде будет отличаться от веса этого тела в воздухе?
     Ответ:     В 5 раз меньше.

21.
     Давление воды в кранах водопровода на высоте 10 м над уровнем земли равно 250 кПа.
Каково давление в кранах, установленных у основания здания?
     Ответ:      350 кПа.

22.
     Лестница длиной 4 м приставлена к идеально гладкой стене под углом 60º к горизонту.
Коэффициент трения между лестницей и полом 0,33.
На какое расстояние вдоль лестницы может подняться человек, прежде чем лестница начнет скользить?
Массой лестницы пренебречь.
     Ответ:     Прежде чем лестница начнет скользить, человек сможет подняться по ней на расстояние 2,29 м.

23.
     На нити длиной 1 м висит шар радиусом 5 см, опирающийся на вертикальную стену.
Нить образует со стенкой угол 30º и касается шара в точке С.
Определить коэффициент трения шара о стенку?
     Ответ:      Коэффициент трения шара о стену равен 0,22.

24.
     Однородная плоская пластинка имеет форму круга, из которого вырезан круг вдвое меньшего радиуса, касающийся первого круга.
Определить положение центра масс пластинки.
     Ответ:      Центр масс расположен на расстоянии R/6 от центра пластинки.

25.
     В цилиндрический сосуд налиты равные массы ртути и воды.
Общая высота двух слоев жидкостей 29,2 см.
Определить давление на дно сосуда?
     Ответ:      Давление жидкостей на дно сосуда 5440 Па.

26.
     Динамометр, к которому подвешен кусок сплава, состоящего из меди и серебра, показывает в воздухе 2,41 Н, а в воде 2,17 Н.
Определить массу меди и серебра в этом куске?
Выталкивающей силой воздуха пренебречь.
     Ответ:     В куске содержится примерно 210 грамм серебра и 31 грамм меди.

27.
     Определите наименьшую площадь плоской льдины толщиной 0,5 м, способной удержать на воде человека массой 75 кг.
Плотность льда - 900 кг/м³, плотность воды - 1000 кг/м³.
     Ответ:      Минимальная площадь льдины равна 1,5 м².

28.
     Полый железный шар взвешивают в воздухе и керосине.
Показания динамометра соответственно равны 2,59 и 2,16 Н.
Определите объем внутренней полости шара?
Выталкивающей силой воздуха пренебречь.
     Ответ:      Объем полости составляет 0,02 л.

29.
     Тонкая деревянная палочка длиной 20 см закреплена шарнирно верхним концом, а нижним опущена в воду.
Найти длину палочки, погруженную в воду?
Плотность дерева принять равной 800 кг/м³.
     Ответ:      Длина погруженной в воду части палочки равна 11 см.

30.
     Брусок высотой h плавает в жидкости, погрузившись в нее наполовину.
На сколько погрузится в ту же жидкость брусок таких же размеров, но изготовленный из материала вдвое меньшей плотности?
     Ответ:      Второй брусок погрузится в жидкость на четверть высоты.