1. Постройте эскиз графика функции:  .
.
Решение. 
Отсюда график:

2. Найдите все значения числового параметра а, при которых корни уравнения  положительны.
положительны.
Ответ.  .
.
Решение. Если (а+1)=0, то уравнение будет линейным, и его корнем при а=-1 является х=1. Подходит.
Если а?-1, то уравнение будет квадратным. По теореме Виета его корни положительны тогда и только тогда, когда выполняется
 .
.
С учетом первого случая получаем ответ  .
.
3. Общая хорда двух пересекающихся окружностей служит для одной из них стороной правильного вписанного четырехугольника, а для другой стороной правильного вписанного шестиугольника. Найдите расстояние между центрами окружностей, если радиус меньшей окружности равен 10 см?
Ответ.  .
.
Решение.


Рис1. Рис 2.
В этой задаче возможны два варианта расположения центра меньшей окружности: Снаружи и внутри большей окружности. Оба варианта расположения изображены на рисунках 1 и 2. В первом случае расстояние между центрами окружностей равно сумме длин высоты равнобедренного прямоугольного треугольника, из которых сложен вписанный квадрат, и высоты равностороннего треугольника, из которого сложен правильный вписанный шестиугольник. Во втором случае – их разность.
Так как диагональ квадрата является диаметром меньшей окружности, то длина стороны квадрата равна  см, и равна длине общей хорды окружностей. Следовательно, радиус большей окружности равен
см, и равна длине общей хорды окружностей. Следовательно, радиус большей окружности равен  см. Тогда длина первой высоты равна
см. Тогда длина первой высоты равна  см, а длина второй высоты равна
см, а длина второй высоты равна  .
.
4. М. В. Ломоносов тратил одну денежку на хлеб и квас. Когда цены выросли на 20%, на ту же денежку он приобретал полхлеба и квас. Хватит ли той же денежки ему хотя бы на квас, если цены вырастут еще на 20%?
Ответ. Хватит.
Решение. Пусть первоначально квас стоил х% от денежки, а хлеб – (100-х)%. После подорожания цен на 20%, получим следующий баланс 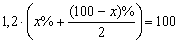 . Отсюда
. Отсюда 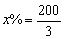 . При двукратном подорожании цен эта величина увеличится в 1,44 раза и достигнет величины 96%, что меньше стоимости денежки.
. При двукратном подорожании цен эта величина увеличится в 1,44 раза и достигнет величины 96%, что меньше стоимости денежки.
5. Существует ли выпуклый многоугольник, число диагоналей которого в 10 раз больше числа его сторон?
Ответ. Существует.
Решение.
Число диагоналей выпуклого многоугольника считается по формуле: 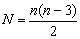 . (Можно считать этот факт известным). Составим и решим уравнение.
. (Можно считать этот факт известным). Составим и решим уравнение. 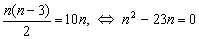 . Таким образом, условию задачи удовлетворяет выпуклый двадцатитрехугольник.
. Таким образом, условию задачи удовлетворяет выпуклый двадцатитрехугольник.
 Олимпиадные задания по математике
Олимпиадные задания по математике

 .
.
