Занимательные задачи по математике
Занимательные задачи по математике с решением
Рассмотрим следующую задачу:
24 спички разделили на три неравные кучки.
Если из первой кучки переложить во вторую столько спичек, сколько было в этой второй кучке, затем из второй кучки переложить в третью столько, сколько было в этой третьей, и наконец из третьей переложить в первую столько спичек, сколько в этой первой кучке осталось, то после всех перекладываний число спичек во всех кучках будет одинаково.
Требуется узнать, сколько было спичек в каждой кучке первоначально.
Решение:
После всех перекладываний в каждой кучке стало по 8 спичек.
Перед этим в первую кучку было добавлено столько спичек, сколько их там имелось, то есть число спИчек в первой кучке было удвоено.
Так как в ней стало 8 спичек, то перед этим там было 4 спички, а 4 спички переложены из третьей кучки.
Следовательно, до последнего перекладывания в первой кучке было 4, во второй – 8, а в третьей – 12 спичек.
Второй раз из второй кучки в третью переложили столько спичек, сколько в третьей имелось. Значит, 12 – это удвоенное число спичек, бывших в третьей кучке до второго перекладывания. Следовательно, можно узнать число спичек в каждой кучке после первого перекладывания: в третьей – 12 : 2 = 6 спичек; во второй – 8 + 6 = 14 спичек; в первой – 4 спички.
Так как первый раз во вторую кучку переложили из первой 14 : 2 = 7 спичек, то первоначально в первой кучке было 11, во второй – 7, а в третьей – 6 спичек.
Еще пример логической задачи по математике
В ящике имеется 12 одинаковых шаров, отличающихся только цветом: 6 красных, 3 белых, 2 зеленых и 1 черный.
Какое наименьшее число шаров нужно взять из ящика наугад (не заглядывая в него), чтобы среди вынутых шаров оказалось:
а) не менее двух шаров одного (любого) цвета?
б) хотя бы три шара одного цвета?
Решение:
Здесь фактически две задачи, но решаются они почти одинаково.
а) В первой задаче требуется определить, сколько нужно вынуть шаров, чтобы среди них обязательно было два шара одного цвета: красного, зеленого или белого, Будем рассуждать следующим образом.
Вынув один шар, мы вынимаем следующий. Он может оказаться того же цвета, что и первый. Но возможен и такой случай, что второй шар иного цвета, чем первый. Так как мы должны быть уверены в том, что среди вынутых шаров обязательно есть два шара одинакового цвета, то нужно рассматривать худший вариант.
Может оказаться, что вынуто уже четыре шара, но все они различных цветов: 1 красный, 1 белый, 1 зеленый и 1 черный. Но если теперь вынуть еще один шар: красный, белый или зеленый (черного уже нет), то в любом случае получим два шара одинакового цвета.
Итак, вынув из ящика 5 шаров, мы обязательно среди них будем иметь два шара одного цвета.
б) При решении второй задачи также рассматриваем худший вариант. Может оказаться, что вынули 2 красных, 2 белых, 2 зеленых и 1 черный, то есть 7 шаров, но среди них нет трех шаров одинакового цвета. Значит, чтобы обязательно было три шара одного цвета, красного или белого, нужно вынуть еще один шар.
Итак, ответ задачи: 8 шаров.
При решении некоторых задач целесообразно составить таблицу или с использовать графы, которые помогут провести рассуждения.
Занимательные задачи по математике. Круги Эйлера
При решении некоторых задач целесообразно для схематического обозначения множеств применять так называемые круги Эйлера.
Множество всех элементов, обладающих определенным свойством, изображают в виде круга.
При рассмотрении двух и более множеств рисуем требуемое число кругов.
Общая часть двух кругов соответствует элементам, которые обладают как свойствами элементов одного множества, так и свойствами элементов другого.
Рассмотрим следующую задачу:
Часть жителей города умеет говорить только по русски, часть – только по белоруски и часть умеет говорить на обоих языках.
По белоруски говорят 85%, по русски 75%.
Сколько процентов жителей говорят на обоих языках?
Решение:
Составим схему:
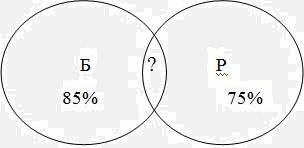
В кружке под буквой «Б» обозначим жителей, говорящих по-белорусски, под буквой «Р» – по-русски. В общей части кружков обозначим жителей, говорящих на обоих языках. Теперь от всех жителей (100%) отнимем кружок «Б» (85%), получим жителей, говорящих только по-русски (15%). А теперь от всех, говорящих по-русски (75%), отнимем эти 15%. Получим говорящих на обоих языках (60%).
Занимательные задачи по математике, решаемые с помощью НОК и НОД чисел
Туристы проехали за 1 день 56 км, а за 2-72км, причем их скорость была одинаковой и выражалась целым числом км/ч, и каждый день они были в пути целое число часов. Найдите скорость, с которой ехали туристы, если она была наибольшей из удовлетворяющих условию задачи.
Решение:
Очевидно, нужно найти НОД (56; 72)
56 = 2 * 2 * 2 * 7; 72 = 3 * 3 * 2 * 2 * 2; НОД (56; 72) = 8
Скорость равна 8 км/ч
Ответ: 8 км/ч.
|
|
Занимательные задачи по математике