Геометрические задачи на логику с решением
Геометрические задачи на логику с решением
Задача 1. Прямоугольник 4 х 9 и квадрат.
Как разрезать прямоугольник со сторонами 4 х 9 на минимальное число частей, чтобы из них сложить квадрат?
Задача 2. Прямоугольник 1 х 3 и симметричное преобразование в квадрат.
Как симметрично разрезать прямоугольник со сторонами 1 х 3 на 9 частей, чтобы из них сложить квадрат?
Задача 3. Греческий крест и квадрат.
Разрезать греческий крест так, чтобы из кусочков можно было сложить квадрат.
а) четырьмя прямыми линиями, используя центральную симметрию;
б) двумя прямыми линиями.
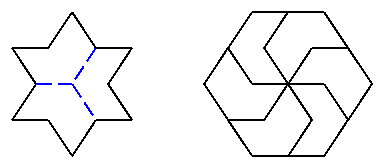
Задача 4. Две шестиконечные звезды и шестиугольник.
Разрезать правильный шестиугольник на наименьшее число частей так, чтобы составить две шестиконечных звезды.
Задача 5. Восьмиугольник и квадрат.
Большинство предложенных ранее головоломок достаточно легко решается с помощью двухполосного метода наложения.
Однако этот метод отнюдь не всегда приводит к желаемому результату.
Например, преобразование правильного восьмиугольника в квадрат, вероятно, легче сделать с помощью метода проб и ошибок, используя симметрию восьмиугольника, чем методом наложения двух полос.
Можно воспользоваться еще одним методом решения задач на разрезание – методом наложения мозаик.
Суть этого очень наглядного и простого метода, позволяющего решать весьма трудные задачи о преобразовании правильных многоугольников, – в наложении двух подходящих (обычно полуправильных) мозаик.
Итак, как преобразовать правильный шестиугольник в квадрат так, чтобы число разрезанных частей было наименьшим?
Решения задач.
Решение задачи 1.
Поскольку площади прямоугольника и квадрата должны быть равны, то сторона квадрата 6.
Поэтому откладываем по 6 на больших сторонах прямоугольника и делаем ступенчатый разрез, о котором можно догадаться, вспомнив о центральной симметрии прямоугольника.
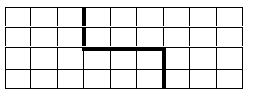
Нетрудно убедиться в том, что при произвольных сторонах прямоугольника ступенчатый разрез не позволит составить равновеликий квадрат.
Решение задачи 2.
Сначала разрезаем 2 квадрата по диагоналям и 4 полученных треугольника располагаем вокруг оставшегося квадрата, приставив части их гипотенуз к его сторонам.
Мысленно соединяем точки прямых углов между собой линиями и вдоль них делаем последние 4 разреза, отрезав от прямоугольных треугольников небольшие тупоугольные треугольники, для которых, как это следует из рисунка, как раз имеются соответствующие местечки.
Решение задачи 3.
 
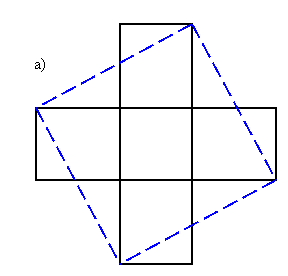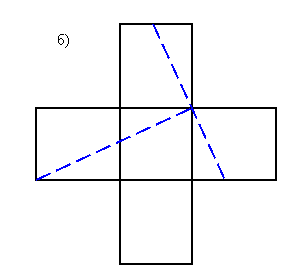
Решение задачи 4.
Решение задачи 5.
 Если попробовать разрезать правильный восьмиугольник так, чтобы сложить полосу, то можно убедиться, что одной из причин неудачи является квадрат со стороной, равной стороне восьмиугольника, половинки которого все время «мешаются».
Это позволяет предположить, что одной из мозаик должна быть очень распространенная среди мозаик полуправильная мозаика из восьмиугольников и квадратов.
Тогда в качестве второй мозаики целесообразно выбрать полуправильную мозаику из квадратов двух размеров, один из которых искомый, а второй тот же, что и в первой мозаике.
Итак, правильный восьмиугольник можно разрезать на 4 одинаковых четырехугольника и квадрат со стороной, равной стороне шестиугольника.
|
|
Логические задачи