Логические задачи на закономерности
Логические задачи на закономерности с решением
Задача 1: Разрезание торта на 8 одинаковых частей. Каково наименьшее число прямолинейных разрезов однородного торта на 8 одинаковых частей?
Торт имеет круглую форму.
Задача 2: Фундаментальное свойство. По какому признаку классифицированы буквы русского алфавита?
1. Б, Г, Д, Й, Р, Ц, Ч, У, Щ, Ъ, Ы, Ь, Я.
2. А, Л, М, П, Т, Ш, Г, Д.
3. В, Е, К, С, 3, Э, Ю.
4. И.
5. Ж, О, Н, X, Ф.
Задача 3: Закономерные телефоны. Один человек предпочитал смысловую память другим ее видам и поэтому всегда, когда надо было запомнить какие-либо числа, пытался находить в них закономерности. Когда его назначили директором завода, он первым делом присвоил каждому начальнику отдела новый четырехзначный номер телефона заводской АТС по известной ему закономерности.
Какой номер телефона у Сергеева, если известны телефонные номера следующих сотрудников:
• Авербух – 7123;
• Белый – 5211;
• Елкин – 5715;
• Жлоп – 4817;
• Иванов – 6103;
• Сергеев – ?
Задача 4: Эпидемия гриппа. В один день 50 человек в поселке с двухтысячным населением простудились и заболели гриппом. Хотя в дальнейшем никто не простужался, разразилась эпидемия гриппа, так как все здоровые в этом поселке считают своим долгом ежедневно навещать больных друзей и при этом заражаются. Грипп был такой, что им болели один день, и на следующий день выздоровевший имел иммунитет и заболеть не мог. Такой же однодневный иммунитет обеспечивала прививка, которую накануне начала эпидемии сделали 100 человек, и вакцина на этом закончилась.
Как долго продлится эпидемия, если каждый житель поселка имел не менее 2 друзей?
Задача 5: Гангстерская разборка. Умудренный опытом прошлых «стрелок», дон Бандитто (главарь преступных кланов города N) отлично знал, что стоит только одному из крутых парней, пришедших базарить, кому-нибудь что-нибудь сказать не то (или даже хотя бы не так на кого-то посмотреть), как тут же начнется пальба без промаха: каждый будет стрелять в ближайшего к себе человека или в одного из одинаково ближайших. Дон Бандитто не мог приказать крутым парням приходить без оружия, так как никто никому не доверял, и ему в том числе. Однако преступный дон сумел-таки обязать всех взять только по одному патрону. Но самой главной заслугой главаря в деле минимизации потерь в живой силе была продуманная расстановка братишек на площади, где планировали провести сходку.
Какое наименьшее число бандитов все же будет вынуждено отойти в мир иной, если всего придет 70 человек?
Решения задач.
Решение задачи 1.
Двумя разрезами можно разделить круглую поверхность торта на 4 равные части.
Третий разрез разделит торт на 2 равные части по толщине,
т. е. он будет проведен в плоскости параллельно верхней и нижней круглым поверхностям.
Решение задачи 2.
Если принимать во внимание лишь существенные особенности букв, игнорируя мелкие детали шрифта, то можно заметить, что во второй строке буквы обладают вертикальной осью симметрии, в третьей – горизонтальной.
Буква "И" обладает центральной симметрией.
Буквы пятой строки обладают всеми предыдущими видами симметрии,
а буквы первой строки несимметричны.
Решение задачи 3.
Первое число (цифра) – число букв в фамилии.
Второе число,(цифра или 2 цифры) - порядковый номер в алфавите начальной буквы фамилии.
Третье число (цифра или 2 цифры) – порядковый номер в алфавите последней буквы фамилии.
Решение задачи 4.
Существование привитых людей, имеющих в первый день эпидемии иммунитет, позволяет эпидемии длиться бесконечно.
Действительно, пусть в первый день эпидемии здоровые В и С навестили больного друга А, причем у С есть иммунитет.
На следующий день заразившегося В навещают выздоровевший и имеющий иммунитет А и С, уже не имеющий иммунитета.
В этот день заражается С, и на следующий день он становится носителем вируса и вторично заражает А.
Эпидемия начинает циклически повторяться и может длиться сколь угодно долго.
Решение задачи 5.
Очевидно, для минимизации потерь нужно, чтобы несколько бандитов стреляли в одного, но, разумеется, с соблюдением условий задачи.
Наилучшим вариантом их размещения хочется сделать круг, чтобы все 69 бандитов, стоящие по окружности, стреляли в одного, стоящего в центре, который тоже убьет одного из них, и все потери составили бы 2 человека. 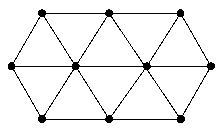 Однако в описанном случае нарушается условие, согласно которому стрельба ведется в ближайшего (или одного из равноудаленных ближайших).
Расстояние между стоящими по окружности будет меньше расстояния до «центрового».
Ясно, что на окружности не разместить более 6 человек, так как отношение длины окружности к ее радиусу есть 2p.
Тогда из семи (6 + 1 =7) человек погибнут 2, а из семидесяти - 20.
Однако это не оптимальное размещение братишек.
Число 6 наталкивает на мысль взять в качестве элементарной ячейки размещения бандитов правильный шестиугольник с седьмым бандитом в центре (или несколько правильных шестиугольников, объединенных в ячейку).
Пусть десять братишек находятся в узлах (углах) двух правильных шестиугольников, наложенных друг на друга так, что их углы совместились с центрами другой фигуры.
Минимальными потери будут, если 8 «наружных» человек стреляют в двух «центровых» бандитов, которые также палят друг в друга.
Из 10 человек погибает только 2; из семидесяти 2 · (70 : 10) = 14.
|
|
Логические задачи