Логические задачи на множества
Логические задачи на множества с решением
Задача 1. 3 белые и 2 черные шляпы.
Как-то три учителя на практикуме решили продемонстрировать ученикам свое умение размышлять.
Они взяли 5 шляп (если кто-то не может представить древнегреческих учителей в шляпах, пусть представит их в разноцветных венках или повязках на голове) - 3 белые и 2 черные - и попросили одного из учеников надеть каждому из них по шляпе.
Ученик мог выбрать каждому произвольный цвет шляпы и надеть ее так, чтобы ни один мудрец не видел цвет своей шляпы.
Ученик надел каждому по белой шляпе, решив, что так сделает выбор учителей труднее.
Учителя договорились о том, что, если кто-либо из них догадается, какого цвета у него шляпа, он сразу же должен заявить об этом.
Вскоре один из них догадался, что у него белая шляпа.
а) Как он рассуждал?
б) Действительно ли ученик выбрал для мудрецов самый трудный вариант?
Задача 2. Построение в ряд.
В другой раз учителя решили провести иную практическую демонстрацию умения рассуждать.
Они стали в ряд (в затылок друг другу) так, что лишь последний в ряду по-прежнему видел шляпы двух других, средний видел только шляпу переднего.
Первый в ряду не видел ни одной шляпы.
Учителя, догадавшиеся о цвете своей шляпы, должны были немедленно и громогласно заявить об этом.
Ученик опять выбрал самый трудный для учителей вариант и надел каждому по белой шляпе, и вскоре один из учителей правильно назвал цвет своей шляпы.
Кто это был?
Задача 3. Утренний прогноз погоды.
1. Если сегодня дождя не будет, то завтра будет ветреная погода.
2. Если же сегодня дождь пройдет, то завтра осадков не будет.
3. Если сегодня будет холодно, то и влажность сегодня будет высокой.
4. Если сегодня будет тепло, то завтра будет безветренно.
5. Если сегодня ветра не будет, то завтра будет тепло.
6. Если же сегодня будет ветрено, то завтра будет дождь, хотя влажность воздуха будет низкой.
7. Если завтра осадков не будет, то завтра будет холодно, а влажность останется такой же, как сегодня.
Какой будет погода сегодня и завтра, без всяких «если»?
Задача 4. Игра в шахматы.
В финале турнира шахматистов встретились представители 6 воинских званий: майор, капитан, лейтенант, старшина, сержант и ефрейтор, разных специальностей: летчик, танкист, артиллерист, минометчик, сапер и связист.
Определите специальность каждого из шахматистов по следующим данным.
В первом туре лейтенант выиграл у летчика, майор у танкиста, а сержант у минометчика.
Во втором туре капитан выиграл у танкиста.
В третьем и четвертом турах минометчик из-за болезни не участвовал в турнире, поэтому свободными от игры оказались капитан и ефрейтор.
В четвертом туре майор выиграл у связиста.
Победителями турнира оказались лейтенант и майор.
Хуже всех выступил сапер.
Задача 5. О профессиях, городах и товарищах.
Три товарища – Иван, Дмитрий и Степан – преподают различные предметы (химию, биологию, физику) в школах Москвы, Ленинграда и Киева.
Известно, что:
1. Иван работает не в Москве, а Дмитрий не в Ленинграде;
2. Москвич преподает не физику;
3. Тот, кто работает в Ленинграде, преподает химию;
4. Дмитрий преподает не биологию.
Какой предмет и в каком городе преподает каждый из товарищей?
Решения задач.
Решение задачи 1.
а) Пусть первым догадался мудрец А.
Он мог рассуждать следующим образом:
«Предположим, что у меня шляпа черная.
Тогда Б видит мою черную шляпу и белую шляпу В и думает, какого цвета его шляпа.
«Если бы моя (Б) шляпа была черной, то В, видя 2 черные шляпы, сразу же заявил бы о белом цвете своей шляпы». Однако В молчит.
Следовательно, Б должен сделать вывод о том, что его шляпа не черная, а белая, и заявить об этом. Однако и Б молчит.
Следовательно, мое исходное предположение о том, что у меня шляпа черная, ложно.
Таким образом, у меня шляпа белая».
б) Если у одного мудреца, например Б, черная шляпа, то А, предположив, что и у него шляпа тоже черная, ожидал бы, что В сразу же догадается, что у него белая шляпа, так как черных шляпы всего 2.
Следовательно еще быстрее догадался бы о цвете своей шляпы, чем в случае, когда у всех белые шляпы.
Если же у двух мудрецов черные шляпы, а у третьего белая, то он моментально об этом догадался бы.
Решение задачи 2.
Пусть А - передний мудрец, Б - второй и В - последний.
Догадался передний мудрец.
Он мог рассуждать, например, так:
«Поскольку последний в ряду мудрец В, который видит 2 шляпы, молчит, то у нас с Б не могут быть одновременно черные шляпы.
Рассуждая аналогично, мудрец Б догадался бы, что у него белая шляпа, если бы у меня была шляпа черная.
Но Б пока молчит, следовательно, у меня шляпа белая».
Если в предыдущих задачах про мудрецов их положение было симметрично и они догадывались о своих лбах и шляпах практически одновременно, то в этой задаче положение первого мудреца, который не видит ни одной шляпы, на первый взгляд самое трудное.
В действительности только он и может догадаться, если все три шляпы белые.
Решение задачи 3.
Из п. 5 и 6 следует, что завтра не может быть одновременно и холодно, и без осадков, и высокая влажность.
Тогда из п. 2 следует, что сегодня дождя не будет.
Тогда из п. 1 следует, что завтра будет ветрено.
Тогда из п. 4 следует, что сегодня будет холодно.
Тогда из п. 3 следует, что сегодня и влажность будет высокой.
Тогда из п. 7 следует, что и завтра влажность будет высокой.
Тогда из п. 6 следует, что сегодня будет безветренно.
Тогда из п. 5 следует, что завтра будет тепло.
Итак, сегодня будет безветренно, холодно, дождь не ожидается, но влажность будет высокой.
Завтра потеплеет и при высокой влажности будет ветрено и дождливо.
Решение задачи 4.
Будем решать задачу, исключая те случаи, которые противоречат какому-либо из условий задачи.
Для удобства решения составим прямоугольную таблицу, в которой по вертикали запишем воинские звания шахматистов, а по горизонтали – их специальности.
Рассмотрим, кто с кем играл первую партию.
В условии сказано, что лейтенант выиграл у летчика, ясно, что лейтенант – не летчик.
Но одновременно с лейтенантом и летчиком на другой доске играл майор с танкистом, значит, лейтенант и не танкист, а майор – не танкист и не летчик.
Учитывая, что на третьей доске играл сержант с минометчиком, мы получаем, таким образом, следующий вывод: лейтенант – не летчик, не танкист и не минометчик.
Ставим в таблице в соответствующих клеточках знак минус, то есть в строке «лейтенант» ставим минусы в 1, 2 и 4-й клеточках (считая слева направо).
В тех же трех столбцах ставим минусы и в строке «майор», ибо и майор – не летчик, не танкист и не минометчик.
По той же причине вписываем минусы в 1, 2 и 4-ю клеточки строки «сержант».
Так как во втором туре капитан выиграл у танкиста, значит, капитан – не танкист, вносим в таблицу еще один минус в соответствующую клеточку (2-я строка, 2-й столбец).
В третьем туре минометчик должен был играть с капитаном, а в четвертом – с ефрейтором, следовательно, минометчик – не капитан и не ефрейтор.
Вписываем в 4-й столбец два минуса в соответствующие клеточки (2 и 6-я, считая сверху вниз).
В четвертом туре майор выиграл у связиста, значит, майор – не связист.
По результатам турнира можно судить, что сапер – не майор и не лейтенант.
Вписав в таблицу и эти последние три минуса, мы получим следующую таблицу:
| Лет-к | Тан-т | Арт-т | Мин-к | Сапер | Св-т | | Майор | – | – | + | – | – | – | | Капитан | + | – | – | – | – | – | | Лейтенант | – | – | – | – | – | + | | Старшина | – | – | – | + | – | – | | Сержант | – | – | – | – | + | – | | Ефрейтор | – | + | – | – | – | – |
По смыслу задачи в каждой строке и в каждом столбце должен быть плюс и только один, ибо каждую специальность имеет только один из шахматистов и каждое воинское звание имеет только один из шахматистов, так как всего шесть различных воинских званий и шести разных специальностей.
Рассмотрим четвертый столбец:
в пяти клеточках стоят минусы, значит, минометчиком является старшина, что обозначим знаком плюс.
Но тогда в. остальных пяти клеточках 4-й строки можно поставить минусы.
Рассмотрим теперь 2-й столбец.
Легко сообразить, что танкистом является ефрейтор.
Поставим плюс во 2-й клеточке последней строки, в остальных клеточках этой строки поставим минусы.
Затем устанавливаем, что летчик – капитан, сапер – сержант, связист – лейтенант, майор – артиллерист.
Можно было рассматривать не столбцы, а строки.
Иногда рассматривают попеременно и строки, и столбцы.
Решение задачи 5.
Выделим три множества: множество имен, множество предметов и множество городов.
Элемент каждого из множеств на рисунке 1 задан своей точкой (буквы на этом рисунке — первые буквы соответствующих слов).
Если две точки из разных множеств характеризуют признаки разных людей, то будем соединять такие точки штриховой линией.
Если же две точки из разных множеств соответствуют признакам одного человека, то такие точки будем соединять попарно сплошными линиями.
Существенно, что по условию задачи для каждой точки любого множества в каждом из остальных множеств найдется одна и только одна точка, ей соответствующая.
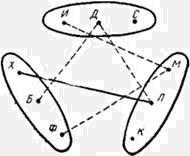
Таким образом, граф на рисунке 1 содержит все заданные в условии элементы множеств и отношения между ними.
Задача на языке графов сводится к нахождению трех «сплошных» треугольников с вершинами в разных множествах.
Рассмотрим граф на рисунке 1.
Напрашивается штриховой отрезок ХД, Действительно, Л соответствует X и, одновременно, Л не соответствует Д, т. е. X не может соответствовать Д.
Итак, используется типичная для такого рода задач операция на графе: если у треугольника с вершинами в трех разных множествах одна сторона сплошная, вторая – штриховая, то третья должна быть штриховой.
Из условия задачи следует равномерность еще одной операции на графе: если какая-то точка соединена штриховыми отрезками с двумя точками во втором множестве, то ее следует соединить с третьей точкой этого множества сплошным отрезком.
Так проводится сплошной отрезок ДФ.
Далее проводится штриховой отрезок ДМ (в треугольнике ДФМ сторона ДФ сплошная, а ФМ – штриховая), ДК сплошным (ДМ и ДЛ штриховые), теперь соединим точки Ф и К сплошным отрезком.
Если в треугольнике с вершинами в разных множествах две стороны сплошные, то третья тоже будет сплошной.
Найден первый «сплошной» треугольник ДФК.
Так, не возвращаясь к тексту задачи, руководствуясь лишь естественными операциями на графе, описанными выше, мы находим решение.
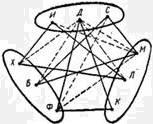
Отметим последовательность,
в которой проводились отрезки: ХД, ДФ, ДМ, ДК, ФК, МС, ИЛ, ХИ, БМ, БС.
Вершины каждого из трех полученных «сплошных» треугольников определяют ответ задачи:
Иван преподает химию в Ленинграде, Дмитрий – физику в Киеве и Степан – биологию в Москве. |
|
 Логические задачи
Логические задачи Логические задачи
Логические задачи