Олимпиадные задания 9 класс с ответами по математике
Задачи олимпиады по математике 9 класс
10 класс 11 класс
1.
Условие: Найти наименьшее значение выражения x + 1/(4x) при
положительных значениях x .
Решение
x + 1/4x = (x + (1/4)/x - 1) + 1 = (x2 - x + 1/4)/x + 1 = ((x - 1/2)2)/x + 1.
Из этого выражения видно, что при положительных значениях переменной
x оно всегда больше единицы, за исключением значения x = 1/2 ,
когда выражение принимает значение 1, которое и будет минимальным
значением выражения при положительных x .
Ответ: 1.00
2.
Доказать, что существует бесконечно много простых чисел.
Задача решается методом от противного.
Предположив, что простых чисел конечное число N, рассматриваем число, следующее за их произведением
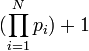
Очевидно, что оно не
делится ни на одно из использованных в произведении простых чисел, давая в остатке 1.
Значит, либо оно само простое, либо оно делится на
простое число, не учтённое в нашем списке.
В любом случае, простых чисел, по крайней мере, N + 1.
Противоречие с
предположением о конечности.
Задачи олимпиады по математике 9 класс
1.
Корень из числа 49 можно извлечь по такой «формуле»: Корень 49 = 4 + Корень 9.
Существуют ли другие двузначные числа, квадратные корни из которых извлекаются аналогичным образом и являются целыми?
Укажите все такие двузначные числа.
2.
ABC – равнобедренный треугольник с вершиной А. угол А = 27°.
Точка D симметрична точке В относительно А. Чему равен угол BCD
3.
Мальчик стоит на автобусной остановке и мёрзнет, а автобуса нет.
Ему хочется пройтись до следующей остановки.
Мальчик бегает вчетверо медленнее автобуса и может увидеть автобус на расстоянии 2 км.
До следующей остановки ровно километр.
Имеет ли смысл идти, или есть риск упустить автобус?
4.
Про числа aи b известно, что a = b + 1. Может ли оказаться так, что a4 = b4?
5.
Какое наименьшее количество клеток квадрата 5 x 5 нужно закрасить, чтобы в любом квадрате 3 x 3, являющемся его частью, было ровно 4 закрашенных клетки?
Ответы и решене задач олимпиады по математике 9 класс
1.
Да, существуют: 64 и 81.
Рассмотрим все двузначные числа, являющиеся квадратами целых чисел.
Корни из чисел 16, 25 и 36 не могут быть извлечены указанным способом, так как квадратные корни из их последних цифр не являются целыми.
Числа 49, 64 и 81 являются решениями.
Ответ в задаче не изменится, если не требовать, чтобы корень был целым. 10a + b = a2 + 2ab + b.
Так как в левой части равенства стоит целое число, то и число, стоящее в правой части, должно быть целым.
Отсюда следует, что b = 0, 1, 4 или 9, то есть a + b - целое число.
2.
Ответ: 90°.
3.
Ответ: имеет смысл идти.
Пусть мальчик пошел к следующей остановке и в какой-то момент заметил автобус.
Скорость автобуса в четыре раза больше скорости мальчика, поэтому за одно и то же время автобус проезжает расстояние в четыре раза больше.
Пусть мальчик пробежит х км, тогда автобус проедет 4х км.
В случае, если они двигаются навстречу друг другу, до встречи с автобусом мальчик пробежит 2/5 км.
Это значит, что, отойдя от остановки не более, чем на 2/5 км, мальчик сможет успеть на автобус, побежав назад.
В случае, если автобус догоняет мальчика, мальчик успеет пробежать 2/3 км до момента, когда автобус его догонит.
Это означает, что он сможет успеть на автобус, если до следующей остановки осталось не более 2/3 км, то есть, если он успел пройти не менее 1/3 км до момента, когда заметил автобус.
Так как, 1/3 < 2/5 , то у мальчика всегда будет возможность успеть на автобус и имеет смысл идти.
4.
Ответ: да, может. Пусть а = 1/2, b = -1/2, тогда a4 = b4 = 1/16.
Можно доказать, что этот пример – единственный (от учащихся это не требуется).
Действительно, a4 = b4 ? |a| = |b|.
Случай a = b невозможен, случай a = -b дает указанный пример.
5.
Ответ: 7 клеток.
|
 Олимпиадные задания по математике
Олимпиадные задания по математике